Generation of Syntactic Quantitative Signals and Alpha Factories (Spaghetti Method)

This is the last of the advanced quant dev series post - next week, we will go back to the basics, and cover the details in how we arrive at the advanced quant backtesting library, which evolved from a rudimentary system consisting of a single signal, single model strategy to a multi signal, multi model strategy system.

Most of the readers who struggle with our current advanced code should really benefit from us going back full circle next week onwards.

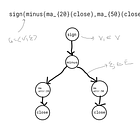
In the advanced quant dev series, we started off with the conceptualisation of trading alpha in different abstract representations, such as mathematical formulas, graphs and visual representations:

Alpha-Encoding Data Structures

For machine trading this would require a convenient translation between the different representations onto computer bits, and we implemented those data structures and algorithms:

Programmatic Quant Alpha Encoding with Python

In order to make use of these data structures, we would require very specific graph traversal algorithms determining the order of evaluation. In addition, recursive thinking was employed to truly appreciate our modelling of the problem:

Traversal Algorithms for Alpha Tree/Graph and Recursion Exercises

In particular, each alpha graph is thought to be composed of sub-alphas, at least in the modelling sense, even if there were no semantic sense for this path of thinking. We then created a no-code quantitative backtesting engine using these building blocks by defining code logic for predetermined primitive structures:

Building a No Code Quantitative Backtest Engine for Machine Trading (with Python)

We demonstrated how to integrate the Russian Doll module to our genetic code:

Integrating the No-Code Quant Backtester into the Russian Doll Engine

In this post, we want to show an application of our module that we have built. We are going to use our module to build a rather simplistic alpha factory. An alpha factory is no strange idea to most alpha research (see link) initiatives. It is the generation of alpha rules, as if they were the yield of an industrial process.

That being said, we are not going into the statistical theory or practical considerations of the utility of these alpha factories - for now we are going to be simply demonstrating the most vanilla application of our module.

We are going to create an algorithm that brute force creates new rules of quantitative `signals’, which is what we call the Spaghetti Method. Akin to throwing Spaghetti at a Wall. Sure, some will stick to the wall, but without doubt a poor approximation to what a good hypothesis of a market edge looks like.

In fact, statistically speaking, if we filter rules using performance cutoffs by this Spaghetti Method, we are guaranteed to overfit data and perform (very) poorly in practice. It is a starting point, however though, and in the future we will discuss some considerations to refine our method. I think this is enough disclaimer. In case you did not pick up the my nuanced message, do NOT use this in your practice. It goes without saying that nothing here is investment advice.

We want to implement a method, that generates signals, in a somewhat arbitrary manner for now. Something that allows us to do this:

>>call
for _ in range(10):
    tr=random_numeric_tree(target_height=3)
    print(tr)

>>output
kentau_19(log(cor_25(volume,low)),median_13(abs(close)))
kentau_25(prod_14(div(high,const_8)),kentau_17(neg(close),kentau_22(const_6,high)))
csrank(median_7(minus(const_7,close)))
ite(gt(open,low),prod_14(cor_25(close,const_11)),neg(cov_20(close,open)))
sign(plus(neg(low),neg(const_15)))
abs(mean_12(kentau_24(high,open)))
log(mult(median_6(high),csrank(const_12)))
prod_14(log(cor_18(volume,volume)))
prod_5(minus(csrank(volume),mult(volume,volume)))
csrank(mean_10(log(close)))
<<

How are we going to do this? We are going to keep it very basic for now, and implement the Spaghetti method. What do we mean to be a ‘Syntactic’ signal? We just mean that it obeys the rules of mathematical grammar. For instance, mult(close,plus(high,volume)) might have nonsensical interpretations, but it is syntactic, insofar as the number of arguments and mathematical rules of the functions defined are not violated. On the other hand, the rule log(high,close) would not be syntactically valid, since logarithms are unary. These rules are really determined by what we say they should be; after all, we are the programmers. For instance, plus(high,low,close) can be interpreted as high + low + close, or we can say that plus is restricted to be a binary operator, and only plus(high,plus(low,close)) should be legal.

I think you get the idea. Again, that the rules make no sense when interpreted is not considered. In other words, we disregard their semantic validity for now. Recall that each node in the alpha graph is associated with a few parameters, in essence the primitive, and sometimes the identifier, which we often say is a `space’ parameter.

For instance, the primitive `neg’ which specifies the negation function has no space parameter, but `cor_12’ has a twelve day space parameter that specifies our correlation function computes the correlation statistic over a sample size of twelve.

Each subtree is also said to be a subalpha, and should therefore have a numerical or boolean output. Of course, in the rule generation algorithm, we want to be able to specify some degree of randomness in the space parameters, so we can explore different functions in our hypothesis space.

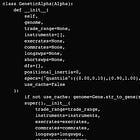
Let’s define the rules in a dictionary:

'''
#primitives.py
Specifies the primitive set
T, F is set of terminals and primitives
space are ephemeral random constants of str, number, enums
    >> use space = None for singletons
    
terminals
    space
    dtype

functions
    space
    params
    dtype_in = () 
    dtype_out = ()

'''
import random
from enum import Enum

class GeneDtype(Enum):
    BOOLEAN = 0
    NUMERIC = 1
    SELECTOR = 2

small_randint = lambda: random.randint(5, 15)
medium_randint = lambda: random.randint(15, 25)

d = lambda x: (lambda : x)
dn = d(None)
d0,d1,d2,d3 = d(0),d(1),d(2),d(3)

'''no params(children)'''
terminals = {
    "const": {"space": small_randint, "dtype_out": GeneDtype.NUMERIC},
    "open": { "space": dn, "dtype_out": GeneDtype.NUMERIC},
    "high": { "space": dn, "dtype_out": GeneDtype.NUMERIC},
    "low": { "space": dn, "dtype_out": GeneDtype.NUMERIC},
    "close": { "space": dn, "dtype_out": GeneDtype.NUMERIC},
    "volume": { "space": dn, "dtype_out": GeneDtype.NUMERIC},
}

'''by definition, has parameters (possibly zero)'''
functions = {
    "abs": {"space": dn, "params": d1, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.NUMERIC},
    "neg": {"space": dn, "params": d1, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.NUMERIC},
    "log": {"space": dn, "params": d1, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.NUMERIC},
    "sign": {"space": dn, "params": d1, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.NUMERIC},

    "csrank": {"space": dn, "params": d1, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.NUMERIC},
    "cszscre": {"space": dn, "params": d1, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.NUMERIC},

    "sum": {"space": small_randint, "params": d1, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.NUMERIC},
    "prod": {"space": small_randint, "params": d1, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.NUMERIC},
    "mean": {"space": small_randint, "params": d1, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.NUMERIC},
    "median": {"space": small_randint, "params": d1, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.NUMERIC},

    "plus": {"space": dn, "params": d2, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.NUMERIC},
    "minus": {"space": dn, "params": d2, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.NUMERIC},
    "mult": {"space": dn, "params": d2, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.NUMERIC},
    "div": {"space": dn, "params": d2, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.NUMERIC},
    "and": {"space": dn, "params": d2, "dtype_in": GeneDtype.BOOLEAN, "dtype_out": GeneDtype.BOOLEAN},
    "or": {"space": dn, "params": d2, "dtype_in": GeneDtype.BOOLEAN, "dtype_out": GeneDtype.BOOLEAN},
    "eq": {"space": dn, "params": d2, "dtype_in": GeneDtype.BOOLEAN, "dtype_out": GeneDtype.BOOLEAN},
    "gt": {"space": dn, "params": d2, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.BOOLEAN},
    "lt": {"space": dn, "params": d2, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.BOOLEAN},
    "ite": {"space": dn, "params": d3, "dtype_in": GeneDtype.SELECTOR, "dtype_out": GeneDtype.NUMERIC},
    "cor": {"space": medium_randint, "params": d2, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.NUMERIC},
    "kentau": {"space": medium_randint, "params": d2, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.NUMERIC},
    "cov": {"space": medium_randint, "params": d2, "dtype_in": GeneDtype.NUMERIC, "dtype_out": GeneDtype.NUMERIC},

    "rsi": {"space": medium_randint, "params": d0, "dtype_in": None, "dtype_out": GeneDtype.NUMERIC},
}

We relax the definition of terminals to contain those that have no arguments. We call these pseudo-terminals, and they behave in the same way as constants, except they implicitly specify computations in the other variables and are functions with no arguments. An example would be the RSI.

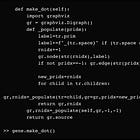
Now, we want to be able to generate random, numerical trees, using the parameter settings specified inside this dictionary. Let’s go ahead and code the algorithms:

We want to generate numerical trees, which are not necessary balanced trees. Sometimes, we can even have `selector’ branches, such as the if-then-else node (ite) that chooses branch 1 when the `if’ statement evaluates to true and branch 2 when `if’ statement evaluates to false. Clearly, the output at the if statement branch needs be boolean type.

We can begin with this overall logic:

import random
from primitives import terminals
from primitives import functions
from primitives import GeneDtype
from gene import Gene

def random_numeric_tree(target_height):
    if target_height == 0:
        return get_leaf()
    qualifiers = [item for item in functions.items() \
        if item[1]["dtype_out"] == GeneDtype.NUMERIC and
            item[1]["params"]() != 0
    ]
    random.seed()
    rand_func = random.choice(qualifiers)
    param_size = rand_func[1]["params"]()
    children = []

    if rand_func[1]["dtype_in"] == GeneDtype.SELECTOR:
        if target_height > 1:
            children.append(
                random_bool_tree(random.randint(1, target_height - 1))
            )
            param_size -= 1 
        else:
            return random_numeric_tree(target_height=target_height)

    for _ in range(param_size):
        children.append(
            random_numeric_tree(target_height=target_height - 1)
        )
    gene = Gene(
        prim=rand_func[0],
        space=rand_func[1]["space"](),
        is_terminal=False, parent=None, children=children
    )
    for child in children:
        child.parent = gene
    return gene

Specifically, we want the boolean tree to have a minimum target height, so that there are logical operands to compare with. A numerical tree can be a leaf node by itself, but boolean trees require arguments to make logical comparisons.

Using similar logic, we can also implement the automatic generation of a boolean tree with specified height: (note you may download the code at the bottom)