Programmatic Quant Alpha Encoding with Python

IN the previous post, we discussed alpha encoding data structures, and referred to their representations in the non-binary tree form, as well as the formulaic form.

Alpha-Encoding Data Structures

In order to go from these abstract representations into machine trading, we need to encode them into bits on the computer. This post implements the algorithm for such a translation. In the NEXT post, we look at recursion exercises and traversal algorithms for the purposes of programmatic evaluation and tree operations.

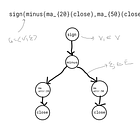
We will use the simple example in the previous post again, for demonstration, but these can quickly become useful even in encoding hefty mathematical formulas. Recalling the simple moving average crossover indicator function:

formula="sign(minus(mean_20(close),mean_50(close)))"

What attributes do we want the tree to have? Recall that each node contains what is known as the primitive, which are the nodes `sign’,`minus’,’mean’,’close’. To distinguish between the 20-ma and 50-ma nodes, the node should optionally contain the space attribute (which can be a number or string, recall our previous gicssector parameter to the neutralize function).

Since a tree node is possibly leaf (terminal) or non-leaf node, we want to have attributes for children, and since the tree is non-binary, instead of left/right pointers we would have an array of variable size.

prim
space: identifies a primitive from its primitive space

children = *[]
parent
is_terminal
size()
height()
depth()

'''
Defines a formulaic quant rule
'''
import numpy as np
class Gene():
    
    def __init__(self, prim, space, is_terminal, parent=None, children=None):
        
        def _extract_numerics(s):
            try:
                return int(s)
            except ValueError:
                try:
                    return float(s)
                except:
                    return s

        self.prim = prim
        self.space = _extract_numerics(s=space) if space else space
        self.is_terminal = is_terminal
        
        self.parent = parent
        self.children = children if children else []

Although the ‘Gene’ object only specifies information at a local node, the root node is the ancestor to every other node and given a pointer to the root Gene(), we essentially have access to the entire tree by traversing the children pointers. Plus, the tree is directed unidirectional, so the back-pointer is not required to go from children to the parent again, but let’s just keep it more flexible and have it for now. This also means that we would need to perform the correct pointer accounting for both parent and children attributes under tree operations (what? don’t worry about tree operations for now).

So how do we go about translating a formulaic alpha string to the Gene data structure? Let’s implement the algorithm, and play

what’s-this-part?

We are going to call the translation using some designated function like

gene=Gene.str_to_gene(formula)

so we should write a static method, and do this recursively. Starting with the base case, we have a pure terminal alpha like `volume’ or ‘const_1’, which corresponds to buying high volume tickers or the buy-and-hold portfolio.

@staticmethod
    def str_to_gene(strgene):
        def index_of(c, s):
            return s.index(c) if c in s else -1
    
        if index_of("(", strgene) < 0:
            return Gene(
                prim=strgene.split("_")[0],
                space=strgene.split("_")[1] if index_of("_", strgene) >= 0 else None,
                is_terminal=True, parent=None, children=None
            )

But likely our alpha is more complicated, and the beginning of the formula would not start with a terminal…

continuing, we would like to extract the strings corresponding to formulaic alphas that are of depth one.

        count = 0
        start = index_of("(", strgene) + 1
        for pos in range(len(strgene)):
            ch = strgene[pos]
            count = count + 1 if ch == "(" else count

            if ch == "," and not "(" in strgene[start:pos]:
                child_strs.append(strgene[start:pos])
                start = pos + 1

            if ch == ")":
                count -= 1
                '''terminal, exclude )'''
                if count == 0:
                    child_strs.append(strgene[start:pos])
                    start = pos + 1
                '''function, include ) '''
                if count == 1:
                    child_strs.append(strgene[start:pos+1])
                    start = pos + 2

‘count’ keeps track of the number of brackets, and the ‘start’ points to the last saved checkpoint in the string parsing. This pointer is initialized to *, and we would like to extract the children between * and <.

sign(*minus(mean_20(close),mean_50(close))<)

If we encounter a comma before an open parenthesis is read, it means that the pos pointer has just ran over a terminal and the substring in between start and pos is a terminal child. Otherwise, the child is another function, and we would use the number of unmatched brackets parsed to determine if the children nodes are leaf or non-leaf.

In our little example, there is just one tree of depth one, so our child_strs contain

[minus(mean_20(close),mean_50(close))]

By the wonders of recursion we can just invoke the same method on this, which now gives child_strs:

[mean_20(close),mean_50(close)]

which we can now iterate the recursion on. We are almost done in fact, since we just need to make the recursive calls and set the child/parent attributes.

But seeing this requires you to be well versed in the dark magic of inception. Don’t worry, we WIRE Immaculate Recursion Exercises into your brain the next post while working with traversal algorithms.

The full algorithm looks like this: