Alpha-Encoding Data Structures

Today, we discuss engineering better quantitative testing infrastructures. In an interview by the legendary quant Jim Simons, he commented on the importance of having good quant-infra systems to test market hypothesis, particularly in the early years of RenTech. This is truly one of the invaluable tools that a quant researcher/trader has at her disposal.

Kicking off a series of lectures on quant trading infrastructures, we will begin with some notes on alpha-encoding data structures. This will be a gentle introduction to alpha trees.

The basic premise of systematic trading is the generation of signals based on rules, that are necessarily part of some `formula’. For instance, a simple trend following system may generate the following digital signal based on the moving average crossover:

\(sign(minus(ma_{20}(close),ma_{50}(close)))\)

The entropy of this bit-flipping system would be rather high, and we may improve our signals by generating increasingly more analog outputs using techniques such as parameter-varying, i.e.

\(plus( \\ sign(minus(ma_{20}(close),ma_{50}(close))), \\ sign(minus(ma_{50}(close),ma_{100}(close))), \\ sign(minus(ma_{100}(close),ma_{200}(close))) \\ )\)

which becomes continuous in its limit. Of course, this is unit-less, and the signal generation would be just a minor (albeit most? important) component of the quant machine. The evolution of digital > analog signal computation would still require forecast and volatility normalizing components to get reasonable portfolio allocations.

But we detract. We are not here to talk about portfolio construction, so let’s stay the course on topic - the point of our above example is that (almost, all?) rule-based trading such as momentum, l/s arbitrage, calendar-effects can be encoded as formulas, and by extension, as programmatic data structures that live inside of computers.

Wouldn’t it suggest then, that we may be able to perform automated evaluation of formulas, and by extension any strategy? Wouldn’t it suggest then, that given some hypothesis about the existence of market anomaly, that we may test it on market data, without explicitly having to write code?

Given the right infrastructure, we can test for the post-earnings-announcement-drift anomaly in the same amount of time as it takes for us to write in pencil the formula:

\(div(epsDifference,std_{12}(epsDifference))\)

or perhaps to neutralize industry effects:

\(neutralize_{gicssector}(div(epsDifference,std_{12}(epsDifference)))\)

Well its certainly possible, assuming you can write the code. With this end-goal in mind, we want to build the designated quant module - and the first step would be in understanding the data structure for formulaic encodings.

Enter graphs (really, trees).

(it has been years since my graph theory class, so forgive me if you are a computer scientist. I may butcher some terms…)

Well a graph is an ordered pair of vertices and edges, denoted

\(G = \langle V,E \rangle\)

where V is the set of vertices and E is the set of edges. Well, really you should watch an introductory video on graphs that introduces graphs as a data structure. In particular, we will be requiring a particularly family of graphs, called trees, which are basically acyclic, directed graphs. Although there is a rich theory on graphs and graph algorithms named Graph Theory, we are using graphs for a very particular purpose, so we will not touch on any of the algorithms such as DFS, BFS, Dijkstra's and so on (we will however, be discussing some traversal algorithms).

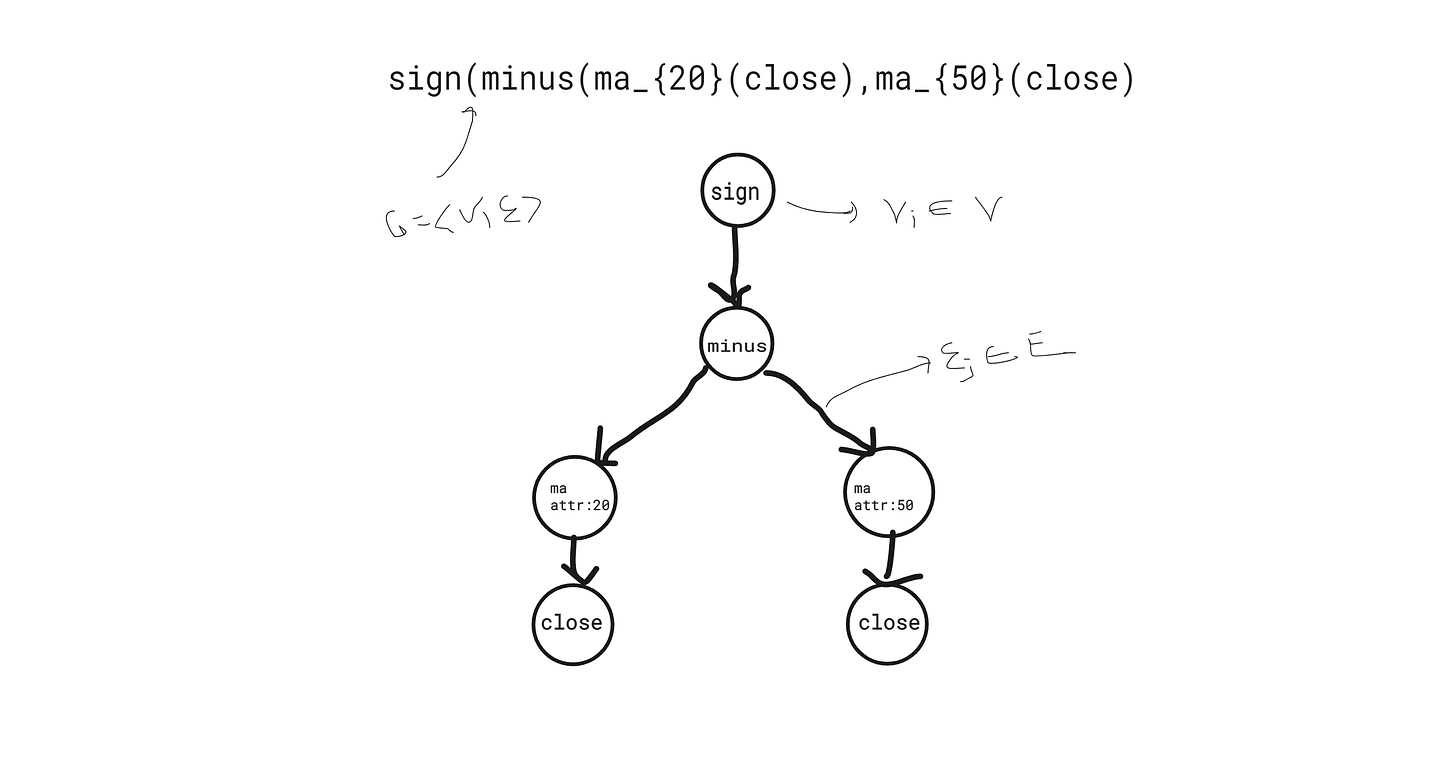
For instance, the digital momentum signal discussed above can be encoded as the following directed, non-binary, unweighted, unidirectional (watch the linked Introduction to Trees video to understand these terms) tree.

Here the root node is the `sign’ vertex, the `close’ vertices are the leaf nodes, and each of the nodes contain what is called a primitive (now crossing over into genetic programming terminology). The `ma’ (moving average) nodes have attributes (now an objected-oriented programming terminology). All together, the momentum signal is encapsulated by this data structure.

That’s pretty much it. We know now that we can encode mathematical formulas (and by extension, most rule-based trading) into a tree structure. In the next lecture, we shall see how to do this on a computer in Python, and paying readers can expect some code (`finally this guy is doing some coding’, I hear you).