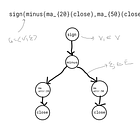
We started off with the conceptualisation of trading alpha in different abstract representations, such as mathematical formulas, graphs and visual representations:
For machine trading this would require a convenient translation between the different representations onto computer bits, and we implemented those data structures and algorithms:
In order to make use of these data structures, we would require very specific graph traversal algorithms determining the order of evaluation. In addition, recursive thinking was employed to truly appreciate our modelling of the problem:
In particular, each alpha graph is thought to be composed of sub-alphas, at least in the modelling sense, even if there were no semantic sense for this path of thinking.
Before we go on, I want to get a sense of something (please also do the post cognitive state at the bottom of the post):
As mentioned, the high level goal for all of these in the first place was for programmatic evaluation of said alpha defined to be in the mathematical form. This post ties together the articles so far and demonstrates this goal. For simplicity, we will use an example from this paper:
https://arxiv.org/pdf/1601.00991.pdf
#Alpha#33: rank((-1 * ((1 - (open / close))^1))) We can of course translate this in the equivalent formulaic language that we have defined:
formula="csrank(neg(minus(const_1,div(open,close))))"which is from our alpha documentation in case you can’t remember:
Anyway, so let’s just go ahead and take inventory of what we already have implemented:
import pytz
import requests
import threading
import numpy as np
import pandas as pd
import yfinance as yf
from datetime import datetime
from bs4 import BeautifulSoup
class Gene():
@staticmethod
def str_to_gene(strgene):
#refer to prev
def __init__(self, prim, space, \
is_terminal, parent=None, children=None
):
#refer
def size(self):
#refer
def depth(self):
#refer
def height(self):
#refer
def __repr__(self):
#refer
def eval_term_node(self, insts, dfs, idx):
#let's implement
def eval_func_node(self, insts, dfs, idx):
#let's implement
def evaluate_node(self, insts, dfs, idx):
#let's implement
def make_dot(self):
#referso we just have to implement the programmatic evaluation component. Ok no problem, as we said, we would like to do pre-order evaluation, which means we visit our child nodes first, so that when we compute our own node, we already have the results required, since the inputs on current node are the outputs from the child nodes. If you don’t follow thus far, means you haven’t really read the last post. So…
def evaluate_node(self, insts, dfs, idx):
if self.cache is not None:
return self.cache
for child in self.children:
child.evaluate_node(insts=insts, dfs=dfs, idx=idx)
if self.is_terminal:
res = self.eval_term_node(insts=insts, dfs=dfs, idx=idx)
else:
res = self.eval_func_node(insts=insts, dfs=dfs, idx=idx)
self.cache=res
return resOk so that’s simple enough, if we have some cached results, return the cache, otherwise if there are children to compute, compute them first using pre-order recursion, and then perform the computation, depending on whether I am a leaf or non-leaf node.
Let’s pause, what do we want the variable `res’ to be? Hmm, I mean it really depends, it could be any data structure that stores the results, like dictionaries, numpy lists and so on, but I think a pandas dataframe would be convenient for readability. So before we implement the eval_term_node, eval_func_node functions, let’s figure out what these objects are…
Suppose we would like to test the idea (the alpha encoding ‘csrank(neg(minus(const_1,div(open,close)))) ‘ ) on spy components, let’s get the tickers (I don’t have to explain these code, right?)
res = requests.get("https://en.wikipedia.org/wiki/List_of_S%26P_500_companies")
soup = BeautifulSoup(res.content,'lxml')
table = soup.find_all('table')[0]
df = pd.read_html(str(table))
tickers = list(df[0].Symbol)and let’s get their OHLCV (500 would take forever, so let’s do some threading):
dfs={}
print("data polling")
def poll(ticker):
dobj=yf.Ticker(ticker)##start="2000-01-01",end="2020-01-01")\
dhist=dobj\
.history(start="2000-01-01")\
.reset_index()
if dhist is None or dhist.empty:
return
dhist=dhist.rename(
columns={
"Date": "datetime",
"Open": "open",
"High": "high",
"Low": "low",
"Close": "close",
"Volume": "volume",
})\
.drop(columns=["Dividends","Stock Splits"])
dhist["datetime"]=dhist["datetime"].dt.tz_localize(pytz.utc)
dfs[ticker]=dhist.reset_index(drop=True).set_index("datetime")
threads=[]
for ticker in tickers:
threads.append(threading.Thread(target=poll, args=(ticker,)))
for thread in threads:
thread.start()
for thread in threads:
thread.join()
print("data obtained")
insts=list(dfs.keys())
dfs={inst:dfs[inst] for inst in insts}which now we have the instrument and data parameters for our case study. Let the range of the study be the longest date range based on available data:
start_idx=min([list(df.index)[0] for df in dfs.values()])
end_idx=max([list(df.index)[-1] for df in dfs.values()])
trade_datetime_range = pd.date_range(
start=datetime(start_idx.year, start_idx.month, start_idx.day),
end=datetime(end_idx.year, end_idx.month, end_idx.day),
freq="D",
tz=pytz.utc
)and we would like to make the function call like this:
gene=Gene.str_to_gene(formula)
node_res=gene.evaluate_node(
insts=insts,dfs=dfs,idx=trade_datetime_range
)So we cleared the ambiguity about what object class instances these variables are. Since we got that out of the way, we should now really be asking ourselves how to implement the terminal and function node evaluation, and what they should return. An aside - if you haven’t actually been thinking about these before I brought them up, it means you are not thinking modularly enough…as a programmer you should think of your pieces of code logic as contract specifications that encapsulate certain logic. Maybe that sentence makes no sense to you, but it will in due time when you progress and work with large code systems.
Ok, so back to the function implementations. To answer the question of how the dataframe should look like, perhaps it is good to think about our data. Well, in general, the data length would not be uniform cross sectionally, since they are listed at different timings. We are working with OHLCV data, which has fairly regular sampling, but what if we really wanted to work with irregularly (in time) sampled data, such as Renko bars, earnings data, sentiment of textual corpus et cetera…we would want to align the data as much as possible. This is why we have the different index aligning methods outlined in our alpha documentation. Maybe this is confusing, read the documentation. Essentially, we will align to a common index of daily frequencies, and do the necessary forward shifting and filtering dynamically based on the desired behaviour of the particular primitive.
To maintain integrity of the data, we would be very careful about propagating up the alpha graph any missing/artificially filled data, otherwise we would get unexpected results. We would go very in depth into exactly what we mean in the future, but let’s just move on.
To evaluate a terminal node, this would be very simple, we just need to pack them into a common dataframe:
def eval_term_node(self, insts, dfs, idx):
temp = []
aligner = pd.DataFrame(index=idx)
if self.prim == "const":
for inst in insts: aligner[inst] = self.space
return aligner
if self.prim in ["open", "high", "low", "close", "volume"]:
for inst in insts:
temp.append(aligner.join(dfs[inst][self.prim]))
else:
pass
res = pd.concat(temp, axis=1)
res.columns = list(insts)
return resto evaluate a function node would be quite abit more complicated, particularly if we want our code to be slim, while maintaining the idiosyncratic behaviour of the different function types (if you are lost, please indicate in the poll below):
def eval_func_node(self, insts, dfs, idx):
aligner = pd.DataFrame(index=idx)
chress = [child.cache for child in self.children]
space=self.space
import scipy
def union_idx_op(op, insts, al, win, *chress):
'''e.g. plus'''
res=[]
chidxs = [[] for _ in range(len(chress))]
for inst in insts:
for chidx, chres in zip(chidxs, chress):
chidx.append(chres[inst].dropna().index)
opdf = op(*[chres.fillna(method="ffill") for chres in chress])
for inst, *chidx in zip(insts, *chidxs):
i_res = opdf[inst].loc[sorted(set().union(*chidx))]
res.append(al.join(i_res))
return pd.concat(res, axis=1)
def self_idx_op2(op, insts, al, win, *chress):
return op(chress[0])
def all_idx_op(op, insts, al, win, *chress):
'''e.g. rank'''
return chress[0].fillna(
method="ffill"
).apply(op, axis=1).apply(pd.Series)
if self.prim == "csrank":
func_type,op = all_idx_op, lambda x:scipy.stats.rankdata(x, method="average", nan_policy="omit")
if self.prim == "neg":
func_type,op = self_idx_op2, lambda x:-1*x
if self.prim == "minus":
func_type,op = union_idx_op, lambda a,b:a-b
if self.prim == "div":
func_type,op = union_idx_op, lambda a,b:(a/b).replace([np.inf, -np.inf], np.nan)
res = func_type(op,insts,aligner,space,*chress)
res.columns = list(insts)
res = res[~res.index.duplicated(keep='first')]
return resActually, I am guessing many people would be lost by now, after this post. The code is quite simplistic and elegant, but it would not be easy to conceptualise. I already said we are going to be working at a somewhat advanced level.
So actually we are done. We can just make a function call like this:
formula="csrank(neg(minus(const_1,div(open,close))))"
gene=Gene.str_to_gene(formula)
node_res=gene.evaluate_node(insts=insts,dfs=dfs,idx=trade_datetime_range)
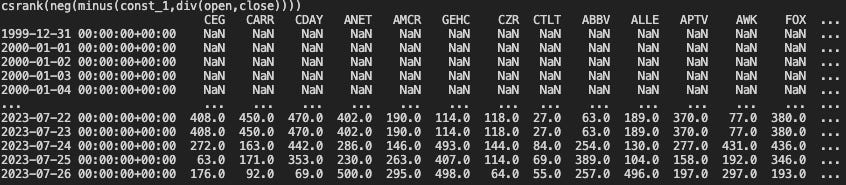
print(gene)
print(node_res)and we get precisely their cross sectional ranks in terms of our alpha specified. We can of course now specify any formula containing the primitives that we have already implemented, and the OHLCV variables.
So yeah, I hope you see the power of the code we have written so far. Based on this post, I want to check back on your cognitive state again:
and
For those who have stuck along and did the work to understand the code, I think this is the post where you start to see the light. Everything changes here.
In the next post, we will in fact integrate this into the Russian Doll Python module, which is our advanced generalised backtesting service class. If we combine the automatic, no-code solution to the Russian Doll, we will essentially have all of the benefits and flexibility of the Russian Doll presented to us with only the requirement that we specify our alpha hypothesis as a mathematical string.
I think that’s enough for now, so here is all the code so far we have implemented in the advanced quant dev series (4 posts now):
(paid):