Quantitative Portfolio Management in Python - AQR EPO 2020 X Russian Doll
P.S. This paper was brought to my attention by my good friend @quant_arb on Twitter who I continue learning from in his terrific Twitter feed, newsletter
and podcast.The last post integrated the quadratic optimizer and the ledoit-wolf constant correlation model into the Russian Doll engine in Python.
Previously, we introduced the benchmark alpha dataset for portfolio optimization.
This week, we added two more alphas and out of sample (up to 2023) performance for these formulaic alphas. Additionally, we introduce and implement the Enhanced Portfolio Optimization method by AQR into the Russian Doll model:
Due to high demand, we will create a post containing instructions on interpretation of formulaic alphas and running the Russian Doll model in future posts. We will add on to the Market Notes and Formulaic Alphas in the coming posts.
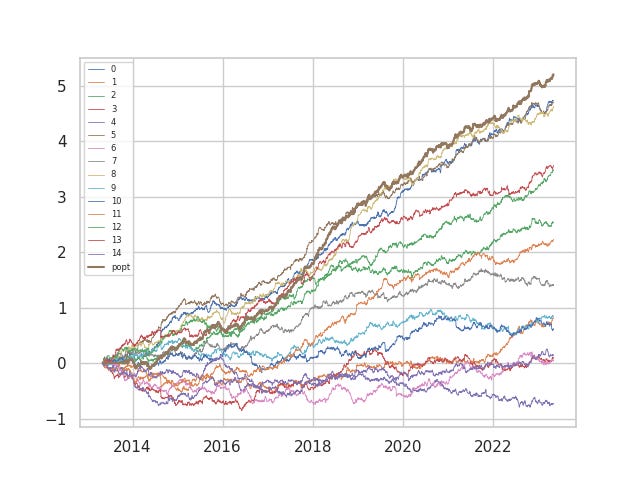
For those questioning whether our formulaic alphas are garbage `statistical mining’, here is the log return curve of the reference benchmark set up to the previous month absent of trade friction. For reference, we started posting these on Aug 22 2021, and 12 of the 15 benchmark alphas presented are faster variants of the alphas that were posted on the platform up to Sep 2021 in our early innings. The other 3 are those posted very recently.
Anyhow, we digress. The purpose of this post is to talk portfolio management, so let's talk portfolio management. Its important to understand in portfolio management, there is no golden rule that applies; context matters. This paper (Dynamic Signal Weighting: When it is Expected to Add Value and When it is Not)
https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1949416
shows that discriminating performance and correlation of the static portfolio matters in the value-add of an active signal weighting approach. Here is some graph and commentary:
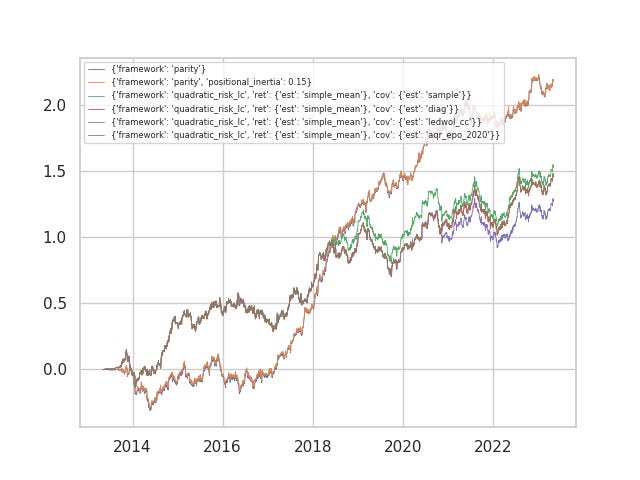
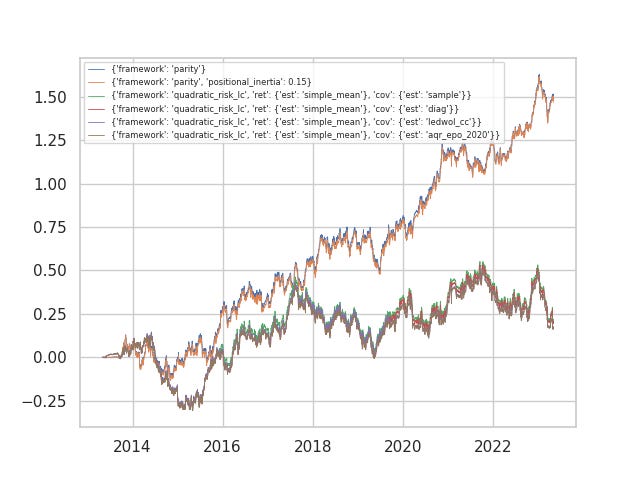
Here one of the datasets are run against various configurations to the Russian Doll (with costs). The parity/static framework performed best, with positional inertia unaffecting the result. In fact, the worst performer was the quadratic-risk ledoit wolf shrinkage model. Between the sample estimator and the aqr_epo_2020 estimator, there are periods when one or the other outperform but their performance is only marginally different. Some questions we may ask: 1) here the alpha dimensionality (p) is only 15, and window (N) size of 90 used to estimate covariance…but what if we increase p and decrease N? We know the sample estimator is notoriously victim to dimensionality curse. 2) Why is the ledoit wolf model markedly worse, is a constant correlation assumption perhaps violated for our group of active alphas?
In fact, between 2014-2018, out quadratic risk portfolios outperformed the parity portfolios. In fact, the parity portfolios stayed underwater for a significant period, while the quadratic risk active portfolio was able to identify the post-cost profitable alphas and almost immediately stay in the green. Clearly, as the L'Hoir paper asserts, discriminatory performance makes the active portfolio outperform. After 2018, all the alphas performed well, and the parity model outpaced the active one.
Our next point is precisely the importance of netting effects when trading multiple active alphas. The popt portfolio presented below (with costs) is precisely the parity portfolio presented on top, but here we plot it against the constituent 15 alphas. About half of the in-silo alphas did not manage to end in the green, but the parity portfolio combining the signals ended well in the green. Signal combination makes the signal to noise ratio higher. Additionally, a less than proportionate increase in the transaction costs incurred due to netting makes unprofitable in-silo statistical arbitrage portfolios profitable. In practice, there would not be fifteen of these, but perhaps a hundred, thousand or even hundreds of thousands of these acting in unison.
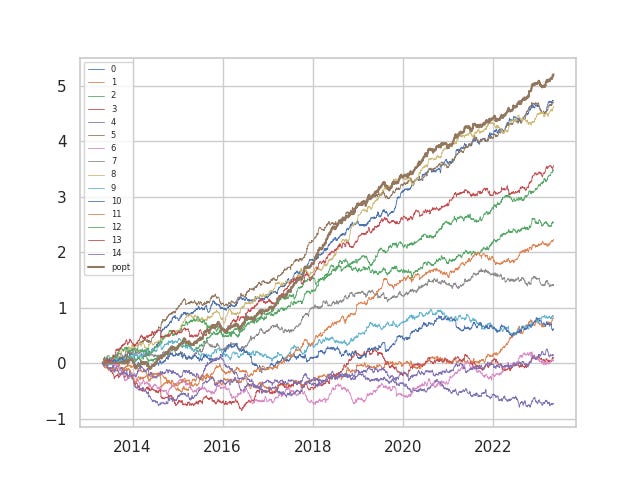
Just how costly is cost? Again, we picked the faster models for demonstration, but the execution can be very expensive. In practice, it depends on the execution model, market impact, rebates and so on and so forth, far beyond what we have covered thus far. The same alphas above are now shown when traded without costs. Of the half that ended in the red with costs, only one ended in the red without costs.
Our next story is a tale of uncertainty. What happens when costs kill even the combined-alpha portfolio? Here, we present results on another dataset.
The different portfolio management variants have the following results (without cost):
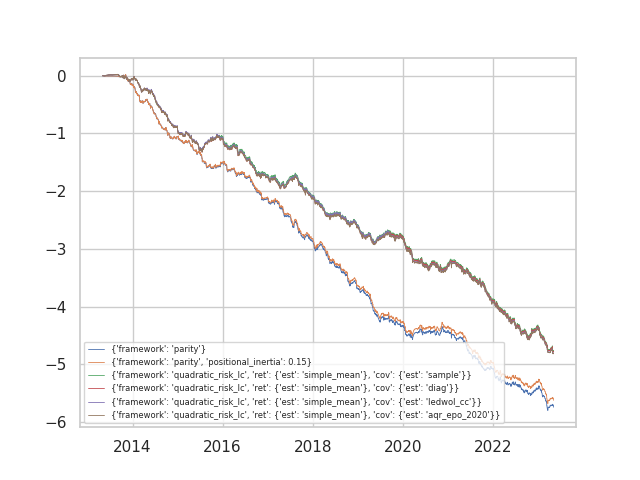
Once again, the parity portfolios perform (almost identically) well, and quadratic risk models perform worse. The covariance estimators perform almost identically in performance. But the returns here are insufficient to overcome the costs of trading so quickly:
When we account for trading costs, the quadratic risk models loses much less money than the parity models. The optimizer knows that we should not trade as often, since our expected gains are not that good in the first place. Notably, positional inertia parity loses less than no inertia parity. Seeing that some level of inertia does not affect cost-less returns and benefits cost-ful returns, even if we are to apply static portfolios, we should always consider adopting some inertia to portfolio turnover.
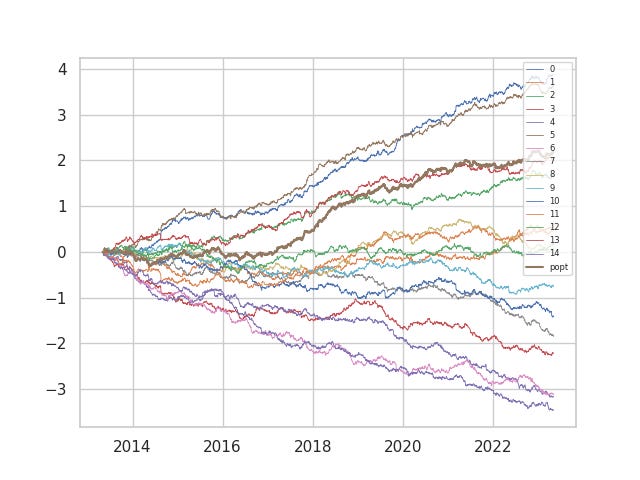
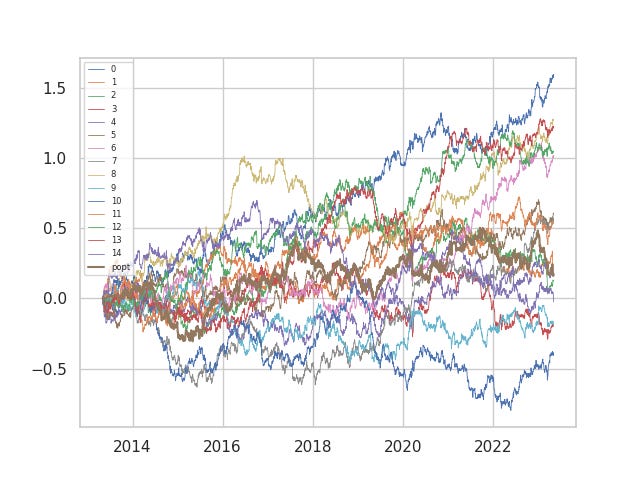
Now, our last lesson: why does the quadratic risk portfolio do so bad? Here are (cost-free) returns of one of the quadratic risk portfolios plotted against its constituents.
When the returns are noisy enough, the quadratic risk model only ends up in the middle of the pack (as opposed to the parity portfolio) in pure returns without cost. It turns out that we fail to effectively capture the benefits of diversification, since the risk optimizer portfolio constantly switches from being concentrated in one portfolio to the another. Another is that the cost penalty in the optimization function stills keeps us operating well below the supposed frontier. We still have a lot to go in improving our estimation of the inputs, in particular the forward returns of our alphas.