Beginner-Intermediate Trader Guide (2) - Trade Modeling

Can I have your number, miss?

In the previous post:

I talked about some of the ideological approaches to becoming a better trader. The three headlines were

1. Read widely, deeply, and do the research

2. Work with Discipline

3. Quantify

The first two points are a bit self-explanatory, but the last point needs tending to. I will give short commentary on the first two points, and then do a case study on the third point on quantification. In fact, we will expound on this last point. After all, teaching ‘discipline’ to traders is not part of my core objective, although it would be nice.

On the first point, we are talking about quality reading. Unfortunately, reading Bloomberg’s article on why markets went down or ‘CTA positioning has been the most bearish since the last decade’ are not examples of helpful reading. The examples I give (AQR, NBER, Rob Carver, Giuseppe Paleologo) are clear examples of sophisticated, clear-thinking individuals/organizations which give useful insight into the enterprise of quantitative trading. Ironically, you are listening to an internet figure `HangukQuant` with a logo H and a tongue sticking down the vertical bar. Not a great start, but you are forgiven.

On the second post, discipline when working with data is key for having robustness in your trading setup. From ideas to frameworks to systems, each hierarchical layer in your trading process need to be subject to that of highest quality. If there is failure to upkeep this level of discipline in each layer, the enterprise must go out of business. Here, quoting The Laws of Trading:

trades…high dimensional space. A given specific trade represents a point in this very large landscape. Since nearly every parameter can be varied in a continuous manner, and since I’ve already defined a good edge as one that’s robust to small parameter variations, the region around a given hyper-profitable trade must also be essentially profitable…there must exist a large region of at least notably high profitability…should be evident why such a large and obvious region cannot exist in a competitive world.

- Agustin Lebron, The Laws of Trading.

A good, robust trade is usually known by many, but the edge in itself is marginal that the extraction of said profits require precision and quality execution. A subset of these people with the skills to extract pnl out of the market implement this trade, which itself exhibits a dynamic landscape.

In the section on quantifying your edge - I explain the importance of having an explainable edge. Such an edge requires both a robust story and model, which in turn require a robust process, which can only be actioned by a robust enterprise. Everything with respect to the inertia of implementation (market and non-market costs) require insight and sampling.

Trade Modeling

The last point raised up, and perhaps the most pertinent one of all is the need to quantify our edge, signal and model. To correctly parameterize our trade, one must first be familiar with the nuances in which the contracts trade under.

The commodities trading world is full of war stories, from hedge fund blowouts to negative prices to squeeze plays and trade busts. Famous is the story of the rookie trader who fails to close out his position in cattle futures. As per contract rules, the financial institution receives a notice of Intention to Deliver, and this trader is sent by the firm to take care of a herd of cattle.

While humorous, such war stories can often have devastating, if not terminal effects on the career of a trader. Avoiding these mistakes require due diligence, the least of understanding contract specifications of which you are involved in. These can be non-trivial, and include but are not limited to information about trade funding, margin, liquidation, swaps, settlements, tick sizes, lot sizes so on and so forth. How is an ETN different from an ETF? Does your position have carry? Can your short positions be bought out? Understanding these specifications are a necessary (but insufficient) requirement for robust practice.

We will do an exercise in due diligence, using linear perpetual contracts in crypto currency markets as an example. Some of the discussions are taken from the Theory chapter on our funding arbitrage lectures. We will look at a simple pair trade doing cross-exchange market making.

The linear perpetuals are derivative contracts - derivative of underlying spot cryptocurrencies. They are linear as opposed to non-linear derivatives, such as options - with payoff structures including non-linear terms (such as max(S-K,0)). The objective of these contracts is to speculate on the price of the underlying coins, where the exposure has a linear payoff to said price movements. In this aspect, it is similar to a futures contract - instead of trading back and forth herds of cows, traders can engage in the speculation of prices of cows using standardized futures contracts. However, unlike these futures contracts, perpetual contracts (like the name suggests) last in perpetuity and have no expiry date. The expiry in futures contract is important - this is the reason as to why there is a relationship between the spot and futures price. Suppose the futures price is much higher than the spot price of cattle - arbitrageurs with the necessary means may buy some cows and short futures at a higher price than the cows are worth. At expiry, he may then deliver said cows, realizing a profit. A similar concept applies to futures contracts in financial instruments that are cash-settled.

How then, do linear perpetuals guarantee a relationship between the spot and derivative prices? This is done using the concept of funding rates, which is a cash flow between traders who have open positions at some regular intervals. It is simply a mechanism that encourages convergence of the perpetual prices to spot prices. When the funding rate is positive (>0), then traders who are long will pay traders who are short.

Without understanding the exact details, intuition should be enough to suggest the signs of funding rate in relation to the price basis between the perpetual and spot prices. In particular, if the perpetual prices were above spot prices, the funding rate should encourage shorts and discourage longs in perpetuals - and thereby the funding rate should be positive (since longs pay shorts). Therefore, this mechanical convergence gives the linear perpetual contracts meaning.

Of course, there will be nuances in these funding specifications. In fact, it turns out that different exchanges compute these funding payments in slightly different methods. Some of these differences may be meaningful, and others might be insignificant, but all of them should be noted. Since this is a general exercise, we shall give a common example, but actual implementations may differ.

Let the underlying spot price be S, where S is a reference spot contract(s). Note that the same coin can trade on multiple exchanges, so S itself may be derived from multiple spot contracts. In many exchanges, this is also called the ‘oracle’ or ‘price index’. The perpetual price is P. We argued that intuition gives:

\(P \geq S \: ? \: sign(fr) = 1 \: : sign(fr) = -1 \)

We will give a top-down run through. Let the funding interval be x hours, say x = 1, 4, 8 and so on. Every x hours, a funding payment fp is made, to the amount of

\(fp = clamp(fr,a,b) * notional\)

where a,b are min and max funding rate limits. notional are the mark-to-market, signed value of positions held. Define ir to be the interest rate, then the funding rate formula is given:

\(fr = \bar P_I + clamp( ir - \bar P_I, 0.05 \%, -0.05 \% )\)

We know all of these terms except for the P-bar-I, which is said to be the weighted premium index. It’s construction is as follows:

\(\bar P_i = \frac{\sum^n_i i \delta_i }{\sum^n_i i}\)

where n is the number of samples taken in a funding interval and:

\(\delta = \frac{M}{S}\)

We have defined S, so defining M:

\(M = \max(P_{bid} - S, 0) - \max(S - P_{ask}, 0)\)

Every single term has been defined except for these P-bid and P-ask terms - understanding this gives us knowledge w.r.t to the cash flows of trading a perpetual contract. Colloquially, P-bid is simply the price received when executing some notional value (Impact margin notional or IMN) on the snapshot of the orderbook. Let x be s.t

\(\sum_{l \leq x} p_l q_l \geq IMN \:\: \&\& \:\: \sum_{l < x} p_l q_l < IMN \)

which is to say x is the lowest depth of the orderbook such that the cumulative dollar size from top of book exceeds IMN. Then -

\(P_{bid} = \frac{IMN}{\sum_{ l < x} q + \frac{IMN - \sum_{l < x} p_l q_l}{p_x}}\)

The formula is unwieldy, and an example is carries much more intuition. Suppose the IMN = 100 dollars, and the orderbook asks has levels:

level 0: 49, 2

level 1: 50, 1

Then we can pick up 98 dollars in size at level 0, and 2 dollars in size at level 1. Accordingly, it is a dollar over weighted volume formula to find a price with market impact:

\(P_{bid} = \frac{100}{2 + \frac{100 - 98}{50}}\)

The P-ask would simply be the same thought exercise on the book’s bid levels.

This discussion sums up the funding aspect of the contracts traded, but in practice there would be further nuances. We have not talked about how mark-to-market value is derived, the trading rules, and so on. We will leave the rest as homework.

Perpetual contracts in cryptocurrencies are used in a variety of known strategies, including local/simple/pure market making, cross exchange arbitrage, funding arbitrage, statistical arbitrage and momentum to name a few. Even the discussions up till here have important implications for these strategies. Let’s state a few.

Since:

\(clamp(x, a, b) = x \: \mathrm{when} \: x \in (a,b)\)

then:

\(fr = \bar P_I + ir - \bar P_I = ir \: \mathrm{when} \: ir - \bar P_I \in (-0.05\%,0.05\%) \)

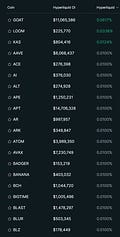
so for a large range of contracts, the effectivefunding rate would be equal to the interest rate. For instance, doing a funding rate sort on hpl website:

we see that most of the contracts in fact exhibit precisely this interest rate figure of 0.01%. Under most circumstances, a long position in these contracts incur slight negative carry. This could be the rough cost of leverage on a long-biased momentum portfolio. This should also indicate that were we to implement cross-exchange arbitrage - non-zero cash flows require at least one of the legs to exceed the clamp bounds.

Understanding edge cases in markets are also helpful. Building a model requires some intuition, and introducing assumptions help to reduce the problem’s dimensionality in order to build a tenable model. We will begin with a common assumption - the one-price frictionless market. In this model, there would cease to be market impact, and we will have

\(P = P_{bid} = P_{ask}\)

then:

\(M = \max(P - S, 0) - \max(S - P, 0) = P - S\)

and

\(\delta = \frac{P - S}{S}\)

which is the perpetual-spot price basis as a proportion of the spot price. It turns out that our intuition was not precisely correct, instead we have:

\(P \geq S \: ? \: sign(\delta) = 1 \: : sign(\delta) = -1 \)

where each delta is a sample for a figure that is inside the funding rate formula.

The opposite of the one-price assumption would be one in which markets are highly illiquid and fragmented. In this case, we have:

\(P_{bid} >> P_{ask}\)

In this scenario, on average we expect

\(\vert \delta \vert >> 0\)

since we can roughly assume that

\(P_{bid} > P \approx S > P_{ask}\)

That is, the more illiquid the market, the greater the likelihood of observing large magnitudes in funding rates. This has implications for price arbitrageurs targeting funding premiums. Again, we observe the no free lunch theorem.

Trading in these illiquid markets, while having the potential for higher premiums, carry unfavorable traits in the form of: a) difficulty in sourcing leverage, b) difficulty in risk management w.r.t to both adverse price movements and unwinding positions, as well as c) capacity issues. The premium itself is a price of scarce liquidity. The compensation is in the form of liquidity risk premiums. With this frame in mind, it might be worth our time to ask: in which trades/exchanges have the most amount of speculators to arbitrageurs? Where are capital flows most favorable in the perspective of the trader harvesting these premiums?

Here, an inspection of the nature of the trade setup and specifications lead us to the source of pnl. The pnl comes from instantaneous flows and swap payments over time. Recall that our example is a pair trade for cross-exchange market making. Since we are working with micro-price differences, our costs (fees and payments) represent a significant proportion of any purported edge.

If you think your costs are negligible relative to your edge, you’re wrong about at least one of them

- Agustin Lebron, The Laws of Trading.

In the book, the author goes on to discuss the four quadrants of cost in the dimensions of linearity and visibility. I will not do you disservice by glossing over these topics, but the law is self explaining. Particularly when your edge is w.r.t to micro-price differences, the constructed model should involve costs.

In our model example, we will again assume the one-price model and instantaneous trade, but that prices can be non-homogenous across exchanges. We will denote with subscripts 1 and 2 for two different exchanges:

\(P_1 - P_2 = (P_1 - S_1) + (S_1 - S_2) + (S_2 - P_2) = a + b + c\)

That is, the price arbitrage between two exchanges consists of three basis terms, one term being the difference in spot oracle prices cross exchange, and the others for the perpetual-spot price basis on each exchange. That is, regardless if it is viewed under a market maker model or a funding arbitrage model - by virtue of trading one contract-and hedging on another, all components are implicitly baked into the trade. We might ignore one of the component or the other, but we must nonetheless recognize it.

By our previous argument, our pair trade would have mechanical convergence in terms a,c - and active convergence of b through liquidity arbitrageurs who are putting on similar trades. If there were some capital flow restrictions and structural dynamics in play, then these terms may diverge for long periods of time.

Assume instantaneous trade, one price model, then an EV model for a pair trade may look something like this. Define:

\(fr_1 = g_1 (P_1,S_1), \: fr_2 = g_2(P_2,S_2),\)

where g’s are respective exchange’s funding formulas, and the prices (and therefore funding rates) are random variables. Let

\(\tau = T - t\)

be the random variable for the holding period, and

\(t_p \leq T\)

be the discrete funding times. Then suppose we go long/short on exchange1/exchange2, we have:

\(\mathbb {EV} = (P_2 - P_1) - \zeta + \sum_{t_p \leq T} (fr_{2,p} - fr_{1,p} )(P_{,p}) \)

where

\(\zeta\)

are our execution fees. Note that this fees depend on how we enter into the pair trade, and which combination of maker and taker fees/rebates we are subject to. On the other hand, for the portfolio state to be invariant, our execution fees need to account for both portfolio entry and exit. The first two terms can be computed immediately (using our assumptions) but the last component requires estimation of the random variables for funding rates and holding time.

Already, we can see interesting concepts at play. For instance, in a cross-exchange market-making trade, upon filling and hedging our positions, we are already subject to inventory. Although our position has no delta, until we can do the opposite end of the trade, we will be subject to funding flows. At zero funding, our portfolio incurs margin costs in the form of opportunity costs and liquidation risk! A positive funding compensation is helpful in balancing these margin costs, and the inventory risk is not so bad after all.

Our instantaneous cash exchange subject us to execution risk and inventory risk thereafter - but if funding differentials were favorable and persistent, then there exists some holding period for which the expected value is positive. This holding period is known as ‘breakevens’. The big assumption, of course, are in the conditions of favorability and persistence.

Given this general pair-trade model, as a trader, we have two concerns. First is in the practicality of this model, and the second is in the assumptions involved. A model can be complete but impracticable. The Black Scholes Merton model prescribes a generative model on option price movements, contingent on a set of assumptions that make them less useful in trading, albeit useful.

The theoretical EV model should then be adjusted until it is practical for computation, under a set of assumptions that nearly hold in practice. For example, our EV model consists of random variables, and as of now - is not computable. We can make it so by:

1. ignoring the random variable terms OR

2. approximating away the random variable terms OR

3. constructing statistical estimators for these random variables.

Once these terms have been removed, then our EV can be computed by a machine, and by extension our trading system. The profitability of the enterprise comes down to our execution and whether our set of assumptions are destructive to our edge. Here is are some of the assumptions (there are many more) we have made in our model:

1. The one price assumption. In practice, we have (prices,volumes).

2. Instantaneous trade assumption, in practice - we have latency

3. Margin constraints

Once these thought exercises and questions have been asked and answered, we are a skip hop and jump away from having a more disciplined trading approach! We can compute this magical EV value that is elusive to traders without frameworks.

Like I said in Part 1…‘there is a better way to make money’. The process is precise, the journey is hard, and may luck succeed your hard work. Happy trading!

These notes are adapted from our funding arbitrage lectures, which can be found here.